class: center, middle, inverse, title-slide # bssm: Bayesian Inference of Non-linear and Non-Gaussian State Space Models in R ### Jouni Helske (joint work with Matti Vihola) ### University of Jyväskylä, Finland ### 9/7/2021 --- ## What are state space models? - The bssm package (Helske, Vihola, 2021) allows fully Bayesian inference of state space models (SSMs) - E.g. structural time series, ARIMA models, generalized linear models with time-varying coefficients, cubic splines, SDEs, ... - In general we have - Observations `\(y=(y_1,\ldots,y_T)\)` with conditional distribution `\(g_t(y_t | \alpha_t)\)` - Latent *states* `\(\alpha=(\alpha_1,\ldots,\alpha_T)\)` with a transition distribution `\(p_t(\alpha_{t+1} | \alpha_t)\)` - Both observations `\(y_t\)` and states `\(\alpha_t\)` can be multivariate - Both distributions can depend on some hyperparameters `\(\theta\)` - Our interest is in the posterior distribution `\(p(\theta, \alpha | y)\)` - Prediction problems `\(p(y_{T+k} | y)\)` and interpolation `\(p(y_t | y)\)` are also straightforward with SSM setting --- ## But wait, what about KFAS? - Compared to the KFAS package (Helske, 2017) for state space modelling: - KFAS is mainly for maximum likelihood inference vs Bayesian approach of bssm - bssm supports more model types (nonlinear models, stochastic volatility models, SDEs) - KFAS uses importance sampling for non-Gaussian models, bssm uses particle filtering (scales better) - bssm is easier to maintain and extend further (written in C++ instead of Fortran) - Creating models is more user-friendly with KFAS (but see `as_bssm` function!) --- ## Bayesian estimation of SSMs - Two important special cases: - Both observation equation and state equation are linear-Gaussian - States `\(\alpha_t\)` are categorical (often called hidden Markov models, not covered by bssm) - In these cases the marginal likelihood `\(p(y | \theta)\)` can be computed easily - Marginalization of latent states results in highly efficient Markov chain Monte Carlo (MCMC) algorithms - Run MCMC targeting the marginal posterior of hyperparameters `\(\theta\)`. - Given samples from `\(p(\theta|y)\)`, simulate latent states from the smoothing distribution `\(p(\alpha | y, \theta)\)`. - `\(\theta\)` is often low dimensional so simple adaptive random walk Metropolis works well. --- ## Bayesian inference for general SSMs - In general, marginal likelihood `\(p(y | \theta)\)` is not analytically tractable. Three routes forward: - Sample both `\(\theta\)` and `\(\alpha\)` directly using, e.g., BUGS (Lunn et al. 2000) or Stan (Stan Development Team 2021). Typically inefficient due to strong correlation structures and high dimensionality of `\(\alpha\)`. - Use (deterministic) approximation of `\(p(y | \theta)\)`, e.g, INLA (Rue et al. 2009), extended Kalman filter (EKF). Fast(er) but biased. Bias is hard to quantify. - Use particle MCMC (Andrieu et al. 2010) where `\(p(y|\theta)\)` is replaced with its unbiased estimator from particle filter. Leads to asymptotically exact inference, but often computationally intensive. Tuning of MCMC nontrivial with respect to number of particles and acceptance rate. --- ## IS-MCMC for state space models - What if we could combine fast approximations and exact methods? - Vihola, Helske and Franks (2020) suggest targeting an approximate marginal posterior of `\(\theta\)`, combined with importance sampling type post-correction (IS-MCMC): - Given `\(\theta\)`, assume that we can compute approximation `\(\hat p(y | \theta) = p(y | \theta) / w(\theta)\)`. - Run MCMC targeting `\(\hat p(\theta | y)\)`, where the marginal likelihood is replaced with the the approximation `\(\hat p(y | \theta)\)`. - For each `\(\theta\)` from approximate marginal, run particle filter to obtain samples of `\(\alpha\)` and unbiased estimate of `\(p(y | \theta)\)`. - We now have weighted samples of `\((\theta, \alpha)\)` from the correct posterior, with weights `\(w(\theta)= p(y | \theta) / \hat p(y | \theta)\)`. --- ## Post-correction - For post-correction we recommend particle filter called `\(\psi\)`-APF (Vihola, Helske, Franks, 2020), which uses the dynamics of the approximating model with look-ahead strategy. - Based on the approximating densities `\(\hat g_t(y_t | \alpha_t)\)`, and `\(\hat p_t(\alpha_{t+1} | \alpha_t)\)` - Produces correct smoothing distribution and unbiased estimate of the marginal likelihood - For state space models supported by `bssm`, often only a small number (e.g. 10) particles is enough for accurate likelihood estimate. - Post-correction is easy to parallelize and the needs to be done only for accepted `\(\theta\)`. --- ## Linear-Gaussian state space models (LGSSM) $$ `\begin{aligned} y_t &= d_t + Z_t \alpha_t + H_t\epsilon_t, \quad \epsilon_t \sim N(0, I)\\ \alpha_{t+1} &= c_t + T_t\alpha_t + R_t \eta_t, \quad \eta_t \sim N(0, I)\\ \alpha_1 &\sim N(a_1, P_1) \end{aligned}` $$ - `\(d_t\)`, `\(Z_t\)`, `\(H_t\)`, `\(c_t\)`, `\(T_t\)`, `\(R_t\)`, `\(a_1\)`, `\(P_1\)` can depend on `\(\theta\)`. - Kalman filter gives us marginal likelihood `\(p(y|\theta)\)`. - Smoothing algorithms give `\(p(\alpha|y,\theta)\)`. - Building general LGSSM and some special cases in bssm: ```r # univariate LGSSM, ssm_mlg for multivariate version ssm_ulg(y, Z, H, T, R, a1, P1, D, C, init_theta, prior_fn, update_fn) # Basic structural time series model bsm_lg(y, sd_level = gamma(1, 2, 10), sd_y = 1, xreg = X, beta = normal(0, 0, 10)) ``` --- ## Non-Gaussian observations - State equation has the same form as in LGSSMs, but observations are non-Gaussian - For example, `\(g_t(y_t | \alpha_t) = \textrm{Poisson}(u_t \exp(d_t + Z_t \alpha_t))\)`, where `\(u_t\)` is the known exposure at time `\(t\)`. - Filtering, smoothing and likelihood available via sequential Monte Carlo (SMC) i.e. particle filtering. - Approximate inference possible via Laplace approximation - Find LGSSM with same mode of `\(p(\alpha | y, \theta)\)` (iteratively) ```r ssm_ung(y, Z, T, R, distribution = "poisson") ssm_mng(...) bsm_ng(...) svm(...) ar1_ng(...) ``` --- ## Bivariate Poisson model with bssm ```r # latent random walk alpha <- cumsum(rnorm(100, sd = 0.1)) # observations y <- cbind(rpois(100, exp(alpha)), rpois(100, exp(alpha))) # function which defines the log-prior density prior_fun <- function(theta) { dgamma(theta, 2, 0.01, log = TRUE) } # function which returns updated model components update_fun <- function(theta) { list(R = array(theta, c(1, 1, 1))) } model <- ssm_mng(y = y, Z = matrix(1, 2, 1), T = 1, R = 0.1, P1 = 1, distribution = "poisson", init_theta = 0.1, prior_fn = prior_fun, update_fn = update_fun) ``` --- ## Other models supported by bssm - Non-linear Gaussian models: $$ `\begin{aligned} y_t &= Z_t(\alpha_t) + H_t(\alpha_t)\epsilon_t,\\ \alpha_{t+1} &= T_t(\alpha_t) + R_t(\alpha_t)\eta_t,\\ \alpha_1 &\sim N(a_1, P_1), \end{aligned}` $$ - Unbiased estimation via particle filtering. - Approximations with mode matching based on extended Kalman filter and smoother. - Models where the state equation is defined as a continuous-time diffusion: $$ \textrm{d} \alpha_t = \mu(\alpha_t) \textrm{d} t + \sigma(\alpha_t) \textrm{d} B_t, \quad t\geq0, $$ - `\(B_t\)` is a Brownian motion, `\(\mu\)` and `\(\sigma\)` are real-valued functions - Observation density `\(p_k(y_k | \alpha_k)\)` defined at integer times `\(k=1\ldots,n\)`. 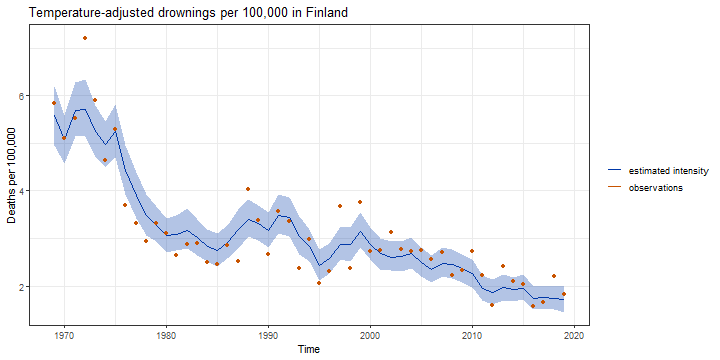- These use user-defined C++ -snippets for model components based on a template provided --- ## Illustration: Modelling deaths by drowning in Finland 1969-2019 - Yearly drownings `\(y_t\)` assumed to follow Poisson distribution - Predictor `\(x_t\)` is (centered) average summer temperature (June to August) - Exposure `\(u_t\)` is the yearly population in hundreds of thousands $$ `\begin{aligned} y_t &\sim Poisson(u_t\exp(\beta x_t + \mu_t)) & t=1,\ldots, T\\ \mu_{t+1} &= \mu_t + \nu_t + \eta_t, & \eta_t \sim N(0, \sigma_\eta^2)\\ \nu_{t+1} &= \nu_t + \xi_t, & \xi_t \sim N(0, \sigma_\xi^2) \end{aligned}` $$ - Hyperparameters `\(\theta = (\beta, \sigma_\eta, \sigma_\xi)\)` - Latent states `\(\alpha_t = (\mu_t, \nu_t)\)` --- ## Estimating the model with bssm ```r data("drownings") model <- bsm_ng( y = drownings[, "deaths"], u = drownings[, "population"], xreg = drownings[, "summer_temp"], distribution = "poisson", beta = normal(init = 0, mean = 0, sd = 1), sd_level = gamma(init = 0.1, shape = 2, rate = 10), sd_slope = gamma(0, 2, 10)) fit <- run_mcmc(model, iter = 20000, particles = 10) summary(fit, TRUE)[,1:4] ``` ``` ## Mean SD SE ESS ## sd_level 0.1029887 0.02195574 0.0007928511 766.8547 ## sd_slope 0.0161829 0.01130342 0.0003732525 917.0944 ## coef_1 0.1109080 0.01743323 0.0005728851 926.0207 ``` --- ## Decrease in drownings after adjusting temperature and population growth <img src="bssm-helske-user2021_files/figure-html/unnamed-chunk-5-1.png" style="display: block; margin: auto;" /> --- ### Thank you! Some references: * Helske, J. (2017). KFAS: Exponential Family State Space Models in R. Journal of Statistical Software, 78(10), 1-39. https://www.jstatsoft.org/article/view/v078i10 * Helske J, Vihola M (2021). bssm: Bayesian Inference of Non-linear and Non-Gaussian State Space Models in R. ArXiv preprint 2101.08492, https://arxiv.org/abs/2101.08492 * Vihola M, Helske J, Franks J (2020). Importance Sampling Type Estimators Based on Approximate Marginal MCMC. Scandinavian Journal of Statistics. https://doi.org/10.1111/sjos.12492 * Lunn, D.J., Thomas, A., Best, N., and Spiegelhalter, D. (2000) WinBUGS — a Bayesian modelling framework: concepts, structure, and extensibility. Statistics and Computing, 10:325–337. * Stan Development Team (2021). Stan Modeling Language Users Guide and Reference Manual, 2.27. https://mc-stan.org * Rue, H., Martino, S. and Chopin, N. (2009). Approximate Bayesian inference for latent Gaussian models by using integrated nested Laplace approximations. Journal of the Royal Statistical Society: Series B, 71: 319-392. https://doi.org/10.1111/j.1467-9868.2008.00700.x * Andrieu, C., Doucet, A. and Holenstein, R. (2010), Particle Markov chain Monte Carlo methods. Journal of the Royal Statistical Society: Series B, 72: 269-342. https://doi.org/10.1111/j.1467-9868.2009.00736.x